(evp4) Ecuación General de Segundo Grado
- orosco julca leonardo

- 9 abr 2019
- 1 Min. de lectura
La forma general de una ecuación de segundo grado es:
Por comodidad, resolveremos la ecuación de tres formas distintas según los valores de los coeficientes bb y cc.
Se llama discriminante, Δ, a
El signo de Δ nos permite conocer el tipo de soluciones de la ecuación:
Si Δ>0, hay dos soluciones reales distintas.
Si Δ=0, hay dos soluciones reales iguales.
Si Δ<0, no hay soluciones reales (hay dos soluciones complejas distintas).
Cuando todas las condiciones se cumplen
Numeros Complejos
Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i).
El Número i
Recordad que b es una raíz cuadrada del número a, si su cuadrado es a. Es decir, b=√a, si b*b =a. Pero sabemos que cualquier número real al cuadrado es mayor o igual que 0, es decir,
Esto implica que la raíz cuadrada de un número negativo no existe. Por ejemplo, si b=√−2, entonces b*b=−2, pero hemos dicho que el cuadrado de un número real no puede ser negativo.
Sin embargo, cualquiera que haya trabajado con ecuaciones cuadráticas (o de segundo grado), sabe que encontrarse con raíces de números negativos es muy habitual. Por esta razón, los matemáticos inventaron números que no son reales y cuyo cuadrado puede ser un número negativo.
Se define la unidad imaginaria i como la raíz cuadrada del número real negativo −1:

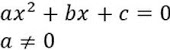












Comentarios